História dos Números
Ensino Fundamental: 5º ano.
Introdução sobre a origem dos números
Você já usou muitas vezes os números, mas será que já parou para pensar sobre:
O modo como surgiram os números?
Como foram as primeiras formas de contagem?
Como os números foram criados, ou, será que eles sempre existiram?
Para descobrir sobre a origem dos números, precisamos estudar um pouco da história humana e entender os motivos religiosos desses criadores. Na verdade, desconhecemos qualquer outro motivo que tenha gerado os números.
Os historiadores são auxiliados por diversas descobertas, como o estudo das ruínas de antigas civilizações, estudos de fósseis, o estudo da linguagem escrita e a avaliação do comportamento de diversos grupos étnicos desde o princípio dos tempos.
Olhando ao redor, observamos a grande presença dos números.
Quanto mais voltarmos na história, veremos que menor é a presença dos números.
O Início do processo de contagem
Os homens primitivos não tinham necessidade de contar, pois o que necessitavam para a sua sobrevivência era retirado da própria natureza. A necessidade de contar começou com o desenvolvimento das atividades humanas, quando o homem foi deixando de ser pescador e coletor de alimentos para fixar-se no solo.
O homem começou a plantar, produzir alimentos, construir casas, proteções, fortificações e domesticar animais, usando os mesmos para obter a lã e o leite, tornando-se criador de animais domésticos, o que trouxe profundas modificações na vida humana.
As primeiras formas de agricultura de que se tem notícia, foram criadas há cerca de dez mil anos na região que hoje é denominada Oriente Médio.
A agricultura passou então a exigir o conhecimento do tempo, das estações do ano e das fases da Lua e assim começaram a surgir as primeiras formas de calendário.
No pastoreio, o pastor usava várias formas para controlar o seu rebanho. Pela manhã, ele soltava os seus carneiros e analisava ao final da tarde, se algum tinha sido roubado, fugido, se perdido do rebanho ou se havia sido acrescentado um novo carneiro ao rebanho. Assim eles tinham a correspondência um a um, onde cada carneiro correspondia a uma pedrinha que era armazenada em um saco.
No caso das pedrinhas, cada animal que saía para o pasto de manhã correspondia a uma pedra que era guardada em um saco de couro. No final do dia, quando os animais voltavam do pasto, era feita a correspondência inversa, onde, para cada animal que retornava, era retirada uma pedra do saco. Se no final do dia sobrasse alguma pedra, é porque faltava algum dos animais e se algum fosse acrescentado ao rebanho, era só acrescentar mais uma pedra. A palavra que usamos hoje, cálculo, é derivada da palavra latina calculus, que significa pedrinha.
A correspondência unidade a unidade não era feita somente com pedras, mas eram usados também nós em cordas, marcas nas paredes, talhes em ossos, desenhos nas cavernas e outros tipos de marcação.
Os talhes nas barras de madeira, que eram usados para marcar quantidades, continuaram a ser usados até o século XVIII na Inglaterra. A palavra talhe significa corte. Hoje em dia, usamos ainda a correspondência unidade a unidade.
Representação numérica
Com o passar do tempo, as quantidades foram representadas por expressões, gestos, palavras e símbolos, sendo que cada povo tinha a sua maneira de representação.
A faculdade humana natural de reconhecimento imediato de quantidades se resume a, no máximo, quatro elementos. Este senso numérico que é a faculdade que permite reconhecer que alguma coisa mudou em uma pequena coleção quando, sem seu conhecimento direto, um objeto foi tirado ou adicionado, à coleção.
O senso numérico não pode ser confundido com contagem, que é um atributo exclusivamente humano que necessita de um processo mental.
"Distingüimos, sem erro e numa rápida vista um, dois, três e mesmo quatro elementos. mas aí para nosso poder de identificação dos números." História Universal dos Algarismos", Georges Ifrah.
Temos também, alguns animais, ditos irracionais, como os rouxinóis e os corvos, que possuem este senso numérico onde reconhecem quantidades concretas que vão de um até três ou quatro unidades. Existe um exemplo célebre sobre um corvo que tinha capacidade de reconhecer quantidades.
 Curiosidade:
Curiosidade: Um fazendeiro estava disposto a matar um corvo que fez seu ninho na torre de observação de sua mansão. Por diversas vezes, tentou surpreender o pássaro, mas em vão: à aproximação do homem, o corvo saía do ninho. De uma árvore distante, ele esperava atentamente até que o homem saísse da torre e só então voltava ao ninho. Um dia, o fazendeiro tentou um ardil: dois homens entraram na torre, um ficou dentro e o outro saiu e se afastou. Mas o pássaro não foi enganado: manteve-se afastado até que o outro homem saísse da torre. A experiência foi repetida nos dias subsequentes com dois, três e quatro homens, ainda sem sucesso. Finalmente, foram utilizados cinco homens como antes, todos entraram na torre e um permaneceu lá dentro enquanto os outros quatro saíam e se afastavam. Desta vez o corvo perdeu a conta. Incapaz de distinguir entre quatro e cinco, voltou imediatamente ao ninho.
Alguns símbolos antigos
No começo da história da escrita de algumas civilizações como a egípcia, a babilônica e outras, os primeiros nove números inteiros eram anotados pela repetição de traços verticais:
| I | II | III | IIII | IIIII | IIIIII | IIIIIII | IIIIIIII | IIIIIIIII |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
Depois este método foi mudado, devido à dificuldade de se contar mais do que quatro termos:
| I | II | III | IIII | IIII
I | IIII
II | IIII
III | IIII
IIII | IIII
IIII
I |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
Um dos sistemas de numeração mais antigos que se tem notícia é o egípcio. É um sistema de numeração de base dez e era composto pelos seguintes símbolos numéricos:
Outro sistema de numeração muito importante foi o da Babilônia, criado a aproximadamente 4 mil anos.
Algumas das primeiras formas de contagem foram utilizadas com as partes do corpo humano, sendo que em algumas aldeias os indivíduos chegavam a contar até o número 33.
O ábaco
O ábaco, em sua forma geral, é uma moldura retangular com fileiras de arame, cada fileira representando uma classe decimal diferente, nas quais correm pequenas bolas
No princípio, os sistemas de numeração não facilitavam os cálculos, logo, um dos instrumentos utilizados para facilitar os cálculos foi o ábaco muito usado por diversas civilizações orientais e ocidentais. No Japão, o ábaco é chamado de soroban e na China de suánpan, que significa bandeja de calcular.
O Sistema de numeração Indo-Arábico
Nosso sistema de numeração surgiu na Ásia, há muitos séculos no Vale do rio Indo, onde hoje é o Paquistão.
O primeiro número inventado foi o 1 e ele significava o homem e sua unicidade, o segundo número 2, significava a mulher da família, a dualidade e o número 3 (três) significava muitos, multidão. A curiosidade sobre os nomes do 3, não deve ter ocorrido por acaso.
| Inglês | Francês | Latim | Grego | Italiano | Espanhol |
|---|
| three | trois | tres | treis | tre | tres |
|---|
| Sueco | Alemão | Russo | Polonês | Hindu | Português |
|---|
| tre | drei | tri | trzy | tri | três |
|---|
Notas históricas sobre a atual notação posicional
Foi no Norte da Índia, por volta do século V da era cristã, que nasceu o mais antigo sistema de notação próximo do atual, o que é comprovado por vários documentos, além de ser citado por árabes (a quem esta descoberta foi atribuída por muitos anos).
Antes de produzir tal sistema, os habitantes da Índia setentrional usaram por muito tempo uma numeração rudimentar que aparece em muitas inscrições do século III antes de Cristo.
Esta numeração tinha uma característica do sistema moderno. Seus nove primeiros algarismos eram sinais independentes:
1, 2, 3, 4, 5, 6, 7, 8, 9
o que significava que um número como o 5 não era entendido como 5 unidades mas como um símbolo independente.
Por muito tempo, estes algarismos foram denominados algarismos arábicos, de uma forma errada.
Ainda existia nesta época a dificuldade posicional e os hindus passaram a usar a notação por extenso para os números, pois não podiam exprimir grandes números por algarismos.
Sem saber, estavam criando a notação posicional e também o zero.
Cada algarismo tinha um nome:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| eka | dvi | tri | catur | pañca | sat | sapta | asta | nava |
|---|
Quando foi criada pelos hindús a base 10, cada dezena, cada centena e cada milhar, recebeu um nome individual:
10 = dasa
100 = sata
1.000 = sahasra
10.000 = ayuta
100.000 = laksa
1.000.000 = prayuta
10.000.000 = koti
100.000.000 = vyarbuda
1.000.000.000 = padma
Ao invés de fazer como hoje, de acordo com as potências decrescentes de 10, os hindus escreviam os números em ordem crescente das potências de 10 por volta do século IV depois do nascimento de Jesus Cristo. Eles começavam pelas unidades, depois pelas dezenas, pelas centenas e assim por diante. O número 3.709 ficava:
| 9 | 700 | 3000 |
|---|
| nove | sete centos | três mil |
|---|
| nava | sapta sata | tri sahasra |
|---|
Poderiamos escrever o número 12.345 como
pañca caturdasa trisata dvisahasra ayuta
pois, 12.345 = 5 + 40 + 300 + 2.000 + 10.000, logo:
5 = pañca
40 = catur dasa
300 = tri sata
2.000 = dvi sahasra
10.000 = ayuta
pañca caturdasa trisata dvisahasra ayuta
Esta já era uma forma especial.
Em virtude da grande repetição que ocorria com as potências de 10, por volta do século V depois do nascimento de Jesus Cristo, os matemáticos e astrônomos hindus resolveram abreviar a notação retirando os múltiplos de 10 que apareciam nos números grandes, assim o número 12.345 que era escrito como:
pañca caturdasa trisata dvisahasra ayuta
passou a ser escrito apenas:
54321 = pañca catur tri dvi dasa
12345 = 5 + 4×10 + 3×100 + 2×1000 + 1×10000
e esta se transformou em uma notação falada e escrita posicional excelente para a época, mas começaram a acontecer alguns problemas como escrever os números 321 e 301.
321 = 1 + 2 x 10 + 3 x 100
321 = dasa dvi tri
301 = 1 + 3 x 100
301 = dasa tri
É lógico que este último número não poderia ser o 31, pois:
31 = 1 + 3 x 10
31 = dasa tri
No número 301 faltava algo para representar as dezenas.
Para construir este material, usamos algumas partes do excelente livro: "Os números: A história de uma grande invenção", Georges Ifrah, Editora Globo, 3a.edição, 1985, com a permissão da Editora.
Notas históricas sobre a criação do zero
Tendo em vista o problema na construção dos números como 31 e 301, os hindus criaram um símbolo para representar algo vazio (ausência de tudo) que foi denominado sunya (a letra s tem um acento agudo e a letra u tem um traço horizontal sobre ela).
Dessa forma foi resolvido o problema da ausência de um algarismo para representar as dezenas no número 301 e assim passaram a escrever:
301 = 1 + ? x 10 + 3 x 100
301 = dasa sunya tri
Os hindus tinham acabado de descobrir o zero.
Porém, estas notações só serviam para as palavras e não para os números, mas reunindo essas idéias apareceram juntos o zero bem como o atual sistema de notação posicional.
Um dos primeiros locais onde aparece a notação posicional é um tratado de cosmologia denominado: Lokavibhaga, publicado na data de 25 de agosto de 458 do calendário juliano, por um movimento religioso hindú para enaltecer as suas próprias qualidades científicas e religiosas. Neste texto, aparece o número 14.236.713 escrito claramente:
| triny | ekam | sapta | sat | trini | dve | catvary | ekakam |
|---|
| três | um | sete | seis | três | dois | quatro | um |
|---|
Escrever tais números na ordem invertida, fornece:
| um | quatro | dois | três | seis | sete | um | três |
|---|
| 1 | 4 | 2 | 3 | 6 | 7 | 1 | 3 |
|---|
Números como 123.000 eram escritos como:
sunya sunya sunya tri dvi dasa
que significa:
zero zero zero três dois um
que escrito na ordem invertida fornece:
um dois três zero zero zero
No texto existe a palavra hindú sthanakramad que significa "por ordem de posição".
Observamos que tal notação posicional já era então conhecida no quinto século de nossa era por uma grande quantidade de cientistas e matemáticos.
Para escrever este material, usamos alguns tópicos do excelente livro: "Os números: A história de uma grande invenção", Georges Ifrah, Editora Globo, 3a.edição, 1985.
Notação Posicional
O sistema de numeração posicional indiano surgiu por volta do século V. Este princípio de numeração posicional já aparecia nos sistemas dos egípcios e chineses.
No sistema de numeração indiana não posicional que aparece no século I não existia a necessidade do número zero.
Notação (ou valor) posicional é quando representamos um número no sistema de numeração decimal, sendo que cada algarismo tem um determinado valor, de acordo com a posição relativa que ele ocupa na representação do numeral.
Mudando a posição de um algarismo, estaremos alterando o valor do número. Por exemplo, tomemos o número 12. Mudando as posições dos algarismos teremos 21.
12 = 1 × 10 + 2
21 = 2 × 10 + 1
O zero foi o último número a ser inventado e o seu uso matemático parece ter sido criado pelos babilônios. Os documentos mais antigos conhecidos onde aparece o número zero, não são anteriores ao século III antes de Cristo. Nesta época, os números continham no máximo três algarismos.
Um dos grandes problemas do homem começou a ser a representação de grandes quantidades. A solução para isto foi instituir uma base para os sistemas de numeração. Os numerais indo-arábicos e a maioria dos outros sistemas de numeração usam a base dez, isto porque o princípio da contagem se deu em correspondência com os dedos das mãos de um indivíduo normal.
Na base dez, cada dez unidades é representada por uma dezena, que é formada pelo número um e o número zero: 10.
A base dez já aparecia no sistema de numeração chinês.
Os sumérios e os babilônios usavam a base sessenta.
Alguma vez você questionou sobre a razão pela qual há 360 graus em um círculo? Uma resposta razoável é que 360=6x60 e 60 é um dos menores números com grande quantidade de divisores, como por exemplo:
D(60) = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}
Os indianos reuniram as diferentes características do princípio posicional e da base dez em um único sistema numérico. Este sistema decimal posicional foi assimilado e difundido pelos árabes e por isso, passou a ser conhecido como sistema indo-arábico.
Nosso sistema de numeração retrata o ábaco. Em cada posição que um número se encontra seu valor é diferente.
O Sistema Romano de Numeração
O sistema de numeração Romano é um sistema decimal, ou seja, sua base é dez. Este sistema é utilizado até hoje em representações de séculos, capítulos de livros, mostradores de relógios antigos, nomes de reis e papas e outros tipos de representações oficiais em documentos. Estas eram as primeiras formas da grafia dos algarismos romanos.
Tal sistema não permite que sejam feitos cálculos, não se destinavam a fazer operações aritméticas mas apenas representar quantidades. Com o passar do tempo, os símbolos utilizados pelos romanos eram sete letras, cada uma com um valor numérico:
| Letra | I | V | X | L | C | D | M |
|---|
| Valor | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
|---|
| Leitura | Um | Cinco | Dez | Cinquenta | Cem | Quinhentos | Mil |
|---|
Estas letras obedeciam aos três princípios:
Todo símbolo numérico que possui valor menor do que o que está à sua esquerda, deve ser somado ao maior.
VI = 5 + 1 = 6
XII = 10 + 1 + 1 = 12
CLIII = 100 + 50 + 3 = 153
Todo símbolo numérico que possui valor menor ao que está à sua direita, deve ser subtraído do maior.
IX = 10 - 1 = 9
XL = 50 - 10 = 40
VD = 500 - 5 = 495
Todo símbolo numérico com um traço horizontal sobre ele representa milhar e o símbolo numérico que apresenta dois traços sobre ele representa milhão.
Fonte: <http://pessoal.sercomtel.com.br/matematica/fundam/numeros/numeros.htm> Acesso: 12 de novembro de 2014


.jpg)
.jpg)
.jpg)
















 Curiosidade: Um fazendeiro estava disposto a matar um corvo que fez seu ninho na torre de observação de sua mansão. Por diversas vezes, tentou surpreender o pássaro, mas em vão: à aproximação do homem, o corvo saía do ninho. De uma árvore distante, ele esperava atentamente até que o homem saísse da torre e só então voltava ao ninho. Um dia, o fazendeiro tentou um ardil: dois homens entraram na torre, um ficou dentro e o outro saiu e se afastou. Mas o pássaro não foi enganado: manteve-se afastado até que o outro homem saísse da torre. A experiência foi repetida nos dias subsequentes com dois, três e quatro homens, ainda sem sucesso. Finalmente, foram utilizados cinco homens como antes, todos entraram na torre e um permaneceu lá dentro enquanto os outros quatro saíam e se afastavam. Desta vez o corvo perdeu a conta. Incapaz de distinguir entre quatro e cinco, voltou imediatamente ao ninho.
Curiosidade: Um fazendeiro estava disposto a matar um corvo que fez seu ninho na torre de observação de sua mansão. Por diversas vezes, tentou surpreender o pássaro, mas em vão: à aproximação do homem, o corvo saía do ninho. De uma árvore distante, ele esperava atentamente até que o homem saísse da torre e só então voltava ao ninho. Um dia, o fazendeiro tentou um ardil: dois homens entraram na torre, um ficou dentro e o outro saiu e se afastou. Mas o pássaro não foi enganado: manteve-se afastado até que o outro homem saísse da torre. A experiência foi repetida nos dias subsequentes com dois, três e quatro homens, ainda sem sucesso. Finalmente, foram utilizados cinco homens como antes, todos entraram na torre e um permaneceu lá dentro enquanto os outros quatro saíam e se afastavam. Desta vez o corvo perdeu a conta. Incapaz de distinguir entre quatro e cinco, voltou imediatamente ao ninho.



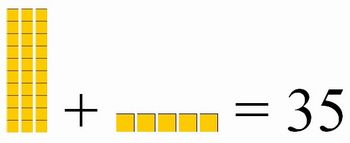
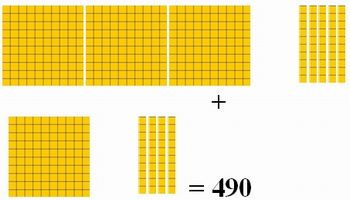

 = 3378
= 3378